目录
电容概念和计算 Capacitance
常见电容类型
- 平行板电容(Parallel Plate Capacitor):
- 决定式推导:
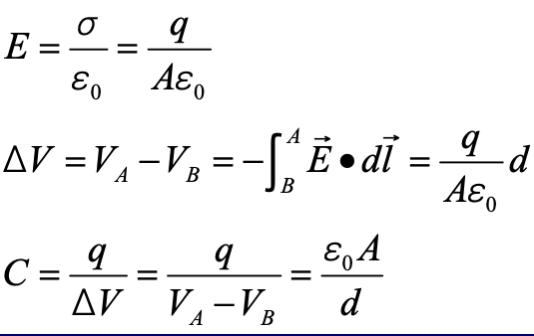
- 决定式推导:
- 圆柱形电容(Cylindrical Capacitor):
- 小结论:带电荷导线径向电场强度:

- 圆柱形电容计算:

- 小结论:带电荷导线径向电场强度:
- 球形电容器(Spherical Capacitor):
- 计算:
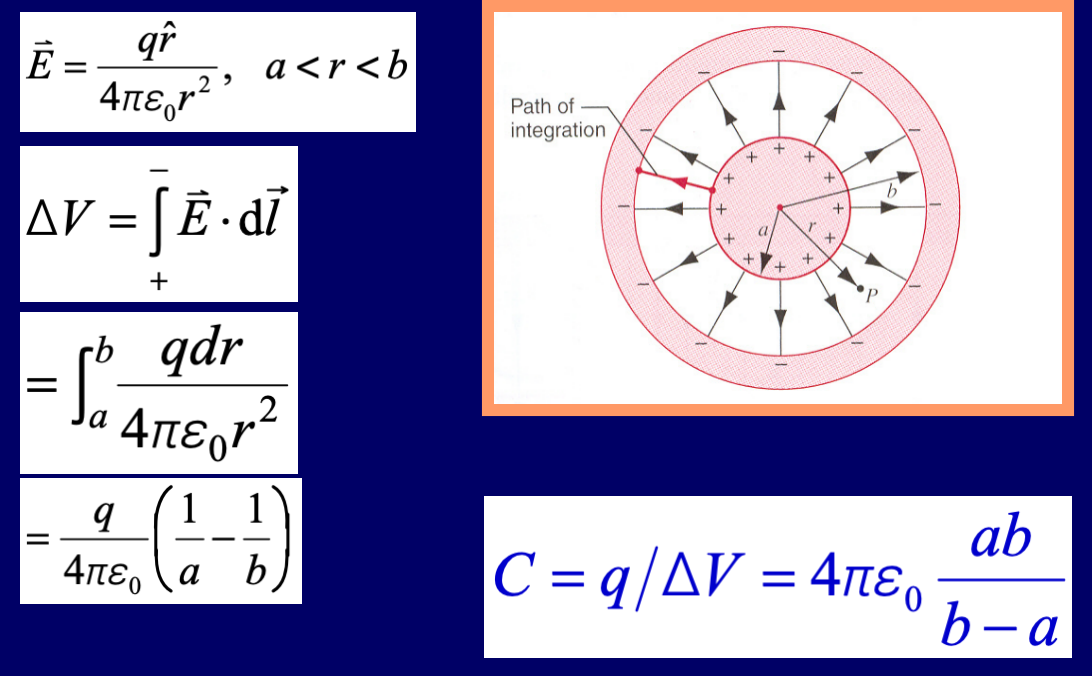
- 孤立球电容:
 计算思想:把外层半径看为无穷大,即b为无穷。
计算思想:把外层半径看为无穷大,即b为无穷。
- 计算:
- 电容串并联:定义推导+等效(整体)替换法
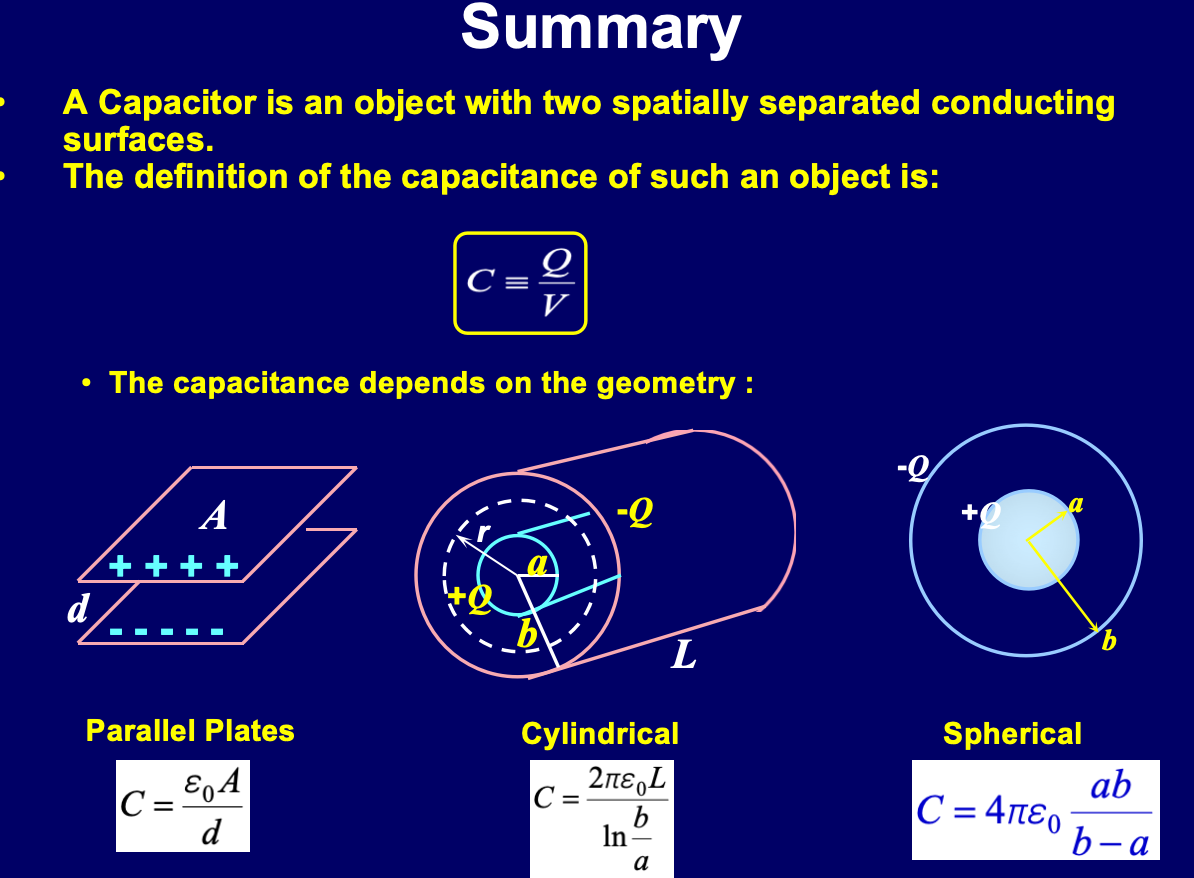
总结:
电容中的电势能U
电势能计算
定义式+积分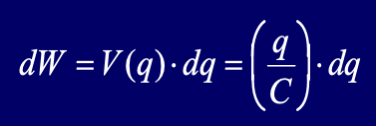
 方法:一般计算从最根本定义式入手,再看看进一步转化为什么。 两种U表示方法:
方法:一般计算从最根本定义式入手,再看看进一步转化为什么。 两种U表示方法: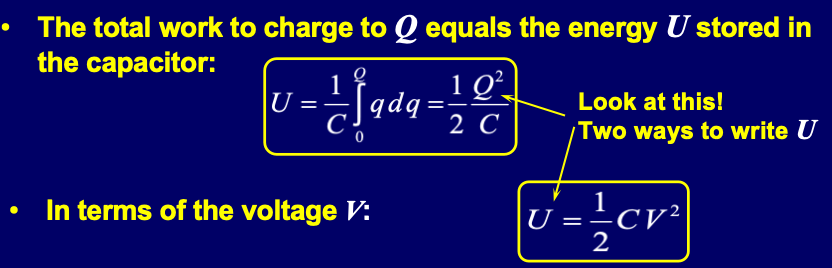 利用公式推导:,
利用公式推导:,
问题:移动电容平行板(断路和通路情况)
断路: 通路:
通路: 能量密度(单位体积):
能量密度(单位体积):
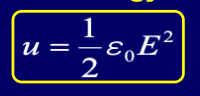 从而在解题时有:
从而在解题时有: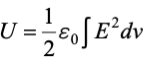 (推导依赖平行板电容模型,但适用广泛) 注意题干各个具体模型,电场是在哪分布、怎么分布的,搞清楚! (有些地方可能连电场都没有)
(推导依赖平行板电容模型,但适用广泛) 注意题干各个具体模型,电场是在哪分布、怎么分布的,搞清楚! (有些地方可能连电场都没有)
电介质(dielectrics)
dielectric constant(介电常数)
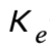 定义:
定义: (和真空电容的比值)
(和真空电容的比值)
🌰:平行电容板加入电介质
- 断电:
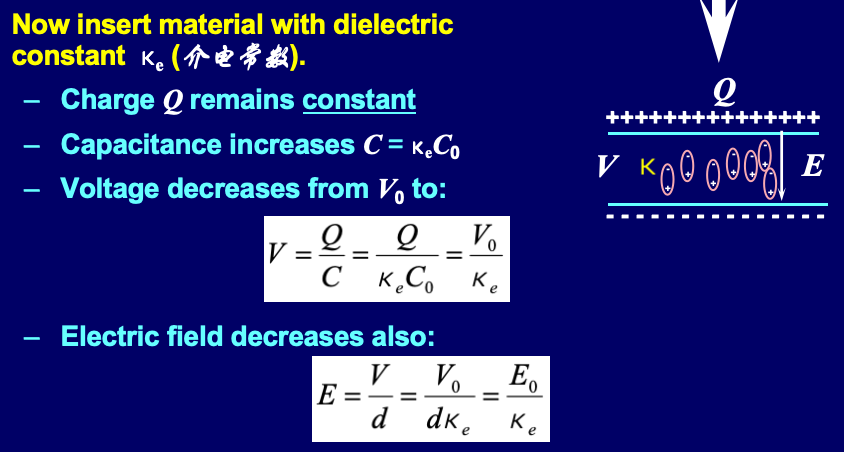
- 通电:
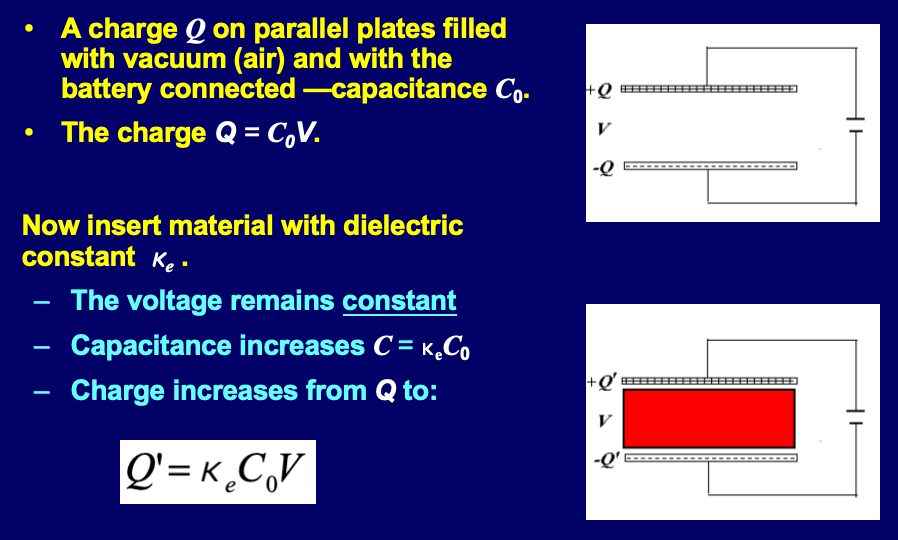 Note:尝试用下面的电介质极化规律
Note:尝试用下面的电介质极化规律 和退极化场
和退极化场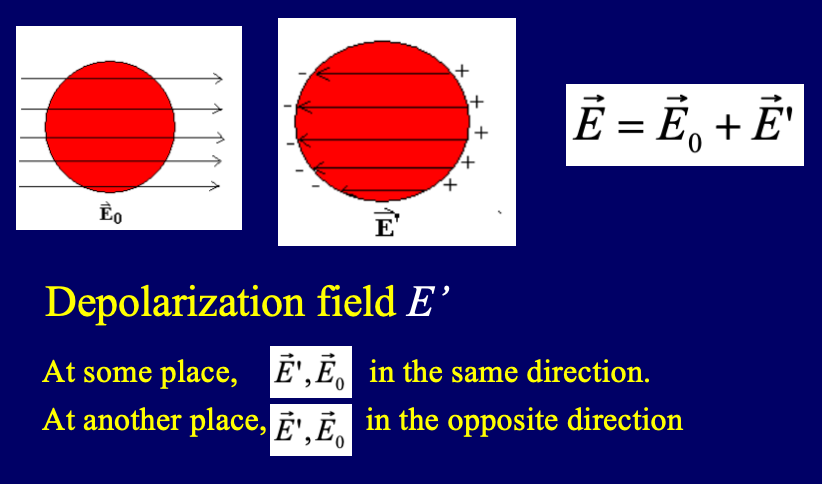 推导电容变化的公式。
推导电容变化的公式。
计算公式总结:(带介电常数) 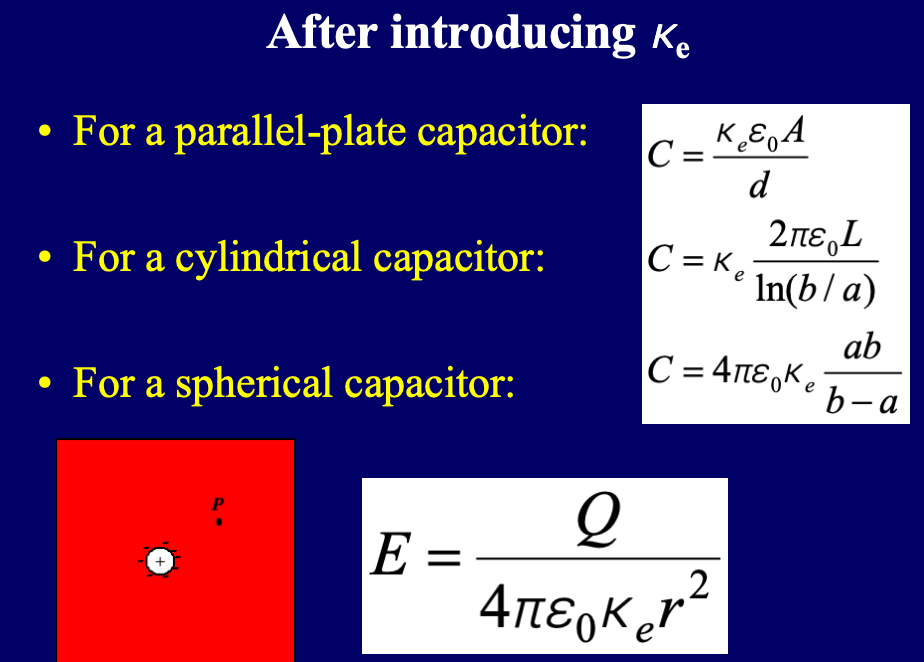
注意对上述变化的宏观理解。
电介质极化
电介质极化(polarization),产生内部电场,抵消原电场。
- 无极分子电介质 Non-polar dielectrics
- Induced electric dipole moment (感生电偶极矩):当外电场作用于一个原本电中性的原子或分子时,电场会使原子或分子中的正负电荷中心发生相对位移,导致电荷的分布不对称,从而产生一个电偶极矩。这个新生成的电偶极矩称为感生电偶极矩。这种现象可以发生在无极分子或非极性原子中,它们在静态条件下不具备内在的电偶极矩。
- Electric displacement polarization (电子位移极化)
- 有极分子电介质Polar dielectrics
- Alignment polarization (取向极化)
- Notes: In high frequency field, Electric displacement polarization (电子位移极化) plays an important role.


- 极化强度矢量(电极化强度)P:
 ()(矢量,方向和l矢量相同)
()(矢量,方向和l矢量相同)
1个难点: 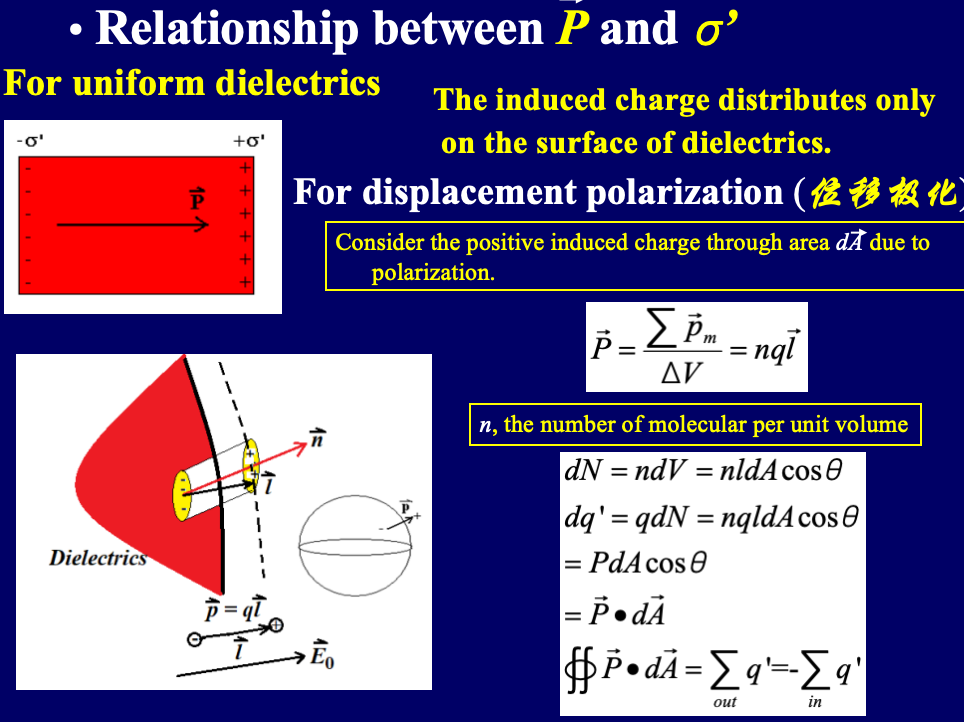
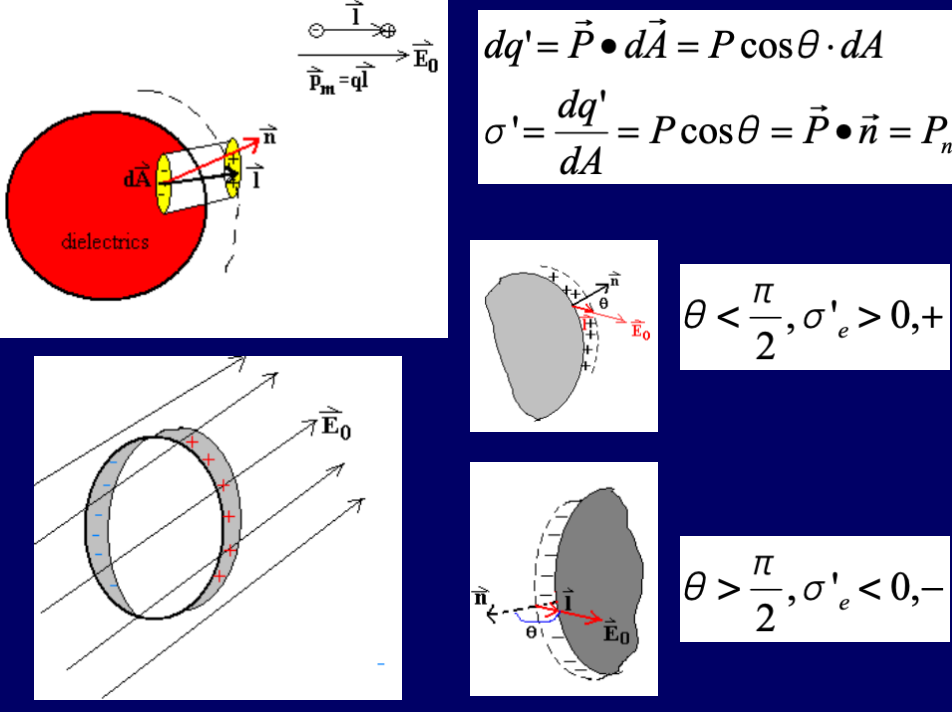
Depolarization Field (退极化场)
 Note:注意这里退极化场计算所乘是最终的总电场强度之和,而不是初始 。 重要:退极化电场常用计算:原电场已知为E_0$,则
Note:注意这里退极化场计算所乘是最终的总电场强度之和,而不是初始 。 重要:退极化电场常用计算:原电场已知为E_0$,则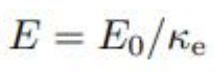 具体应用可见第五周作业。
具体应用可见第五周作业。 
电介质极化规律

Electric Displacement Vector D (电位移矢量) and Gauss’ Law with Dielectrics. 电偶极矩的高斯定律是描述在电偶极场中电位移的高斯定理。它与我们通常理解的电荷分布的高斯定律有所不同。对于一个带有偶极矩的系统,没有净电荷分布,但会有极化电荷的分布。
在电偶极矩的情况下,考虑到极化电场的性质,我们需要引入极化强度 (电偶极矩密度)来描述内部极化效应。其对应的高斯定律公式如下:
这里,表示电位移场, 表示自由电荷体密度。然而在电偶极子或偶极矩密度的情况下,我们通常没有自由电荷密度,只有极化电荷密度。因此我们可以进一步使用极化强度 来定义电位移场。
使用极化强度的高斯定律
在材料内部的电场可通过以下公式描述:
和
极化电荷的高斯定律
对于电偶极矩分布来说,可以用以下形式表达高斯定律:
其中:
- 是极化产生的束缚电荷密度。
物理含义
这种形式的高斯定律表明,在一个偶极矩分布中,偶极产生的电荷并不是真正的自由电荷,而是由于极化产生的束缚电荷。这些束缚电荷分布在材料表面或内部,导致内部产生一个反向的退极化场,用以抵消一部分极化电场。 

推导: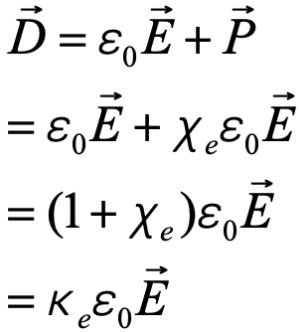
需要补充:电位移矢量的高斯定律 极化率公式 自由电荷和束缚电荷相抵消,得到总的电荷量体密度 极化强度矢量:
如何求散度:gpt

