Leftest Heap VS Skew Heap#

定义#

左偏堆#

先来看左偏堆对dist的定义： 一个左偏堆的结点维护了左右子堆的地址、自身的键值、和一个“距离(dist)”。

struct LeftistHeapNode {
    ElementType val;
    int dist;
    LeftistHeapNode * ls, * rs;
};

一共定义了四个”部件“，不难类比到，左偏堆对dist的维护相当于AVL Tree对height的维护，左偏堆->斜堆，可以类比为 AVL ->splay，是一种对维护信息负担的化简。 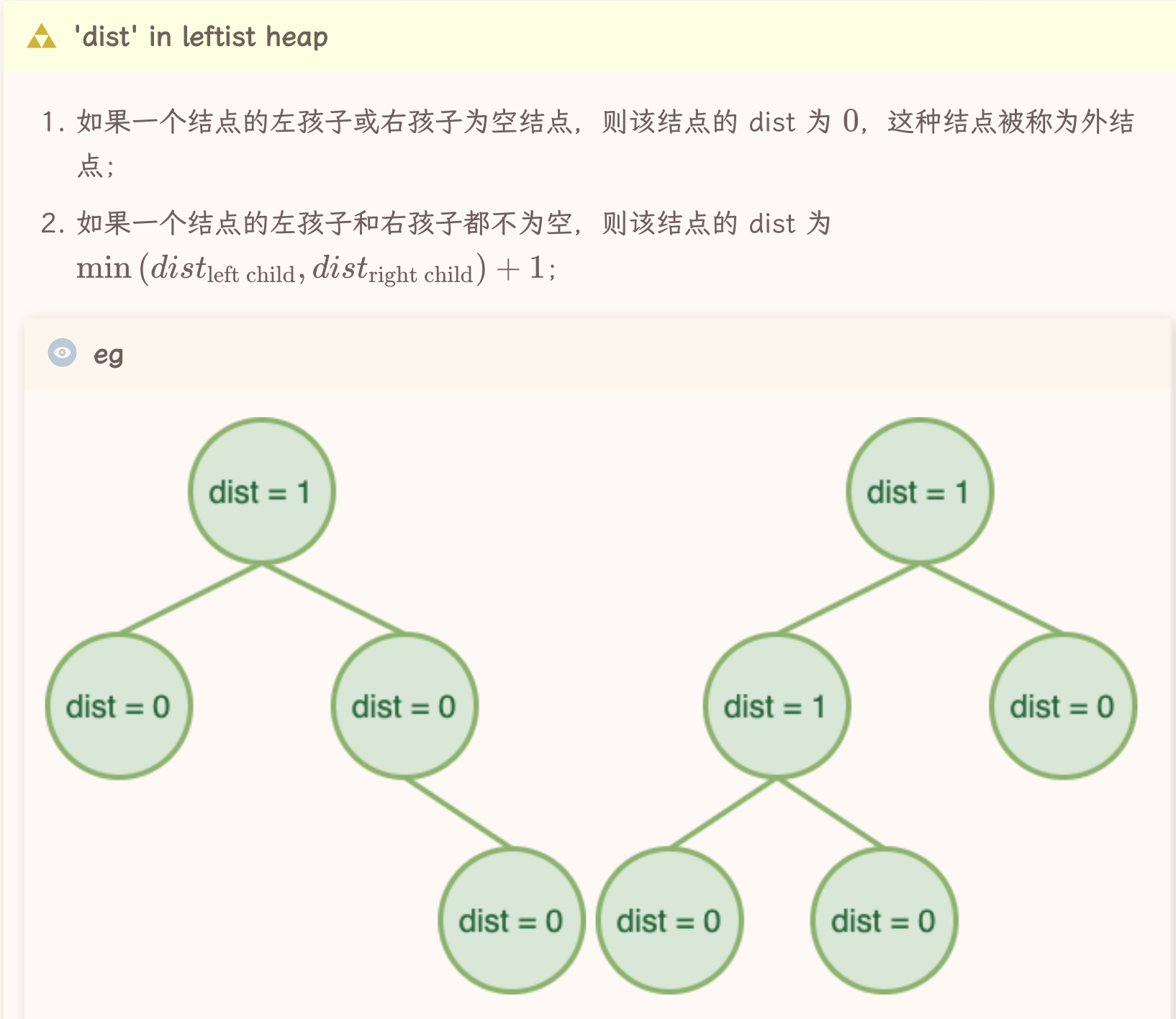从第二点可以看出，dist是递归定义的。 从dist定义左偏堆：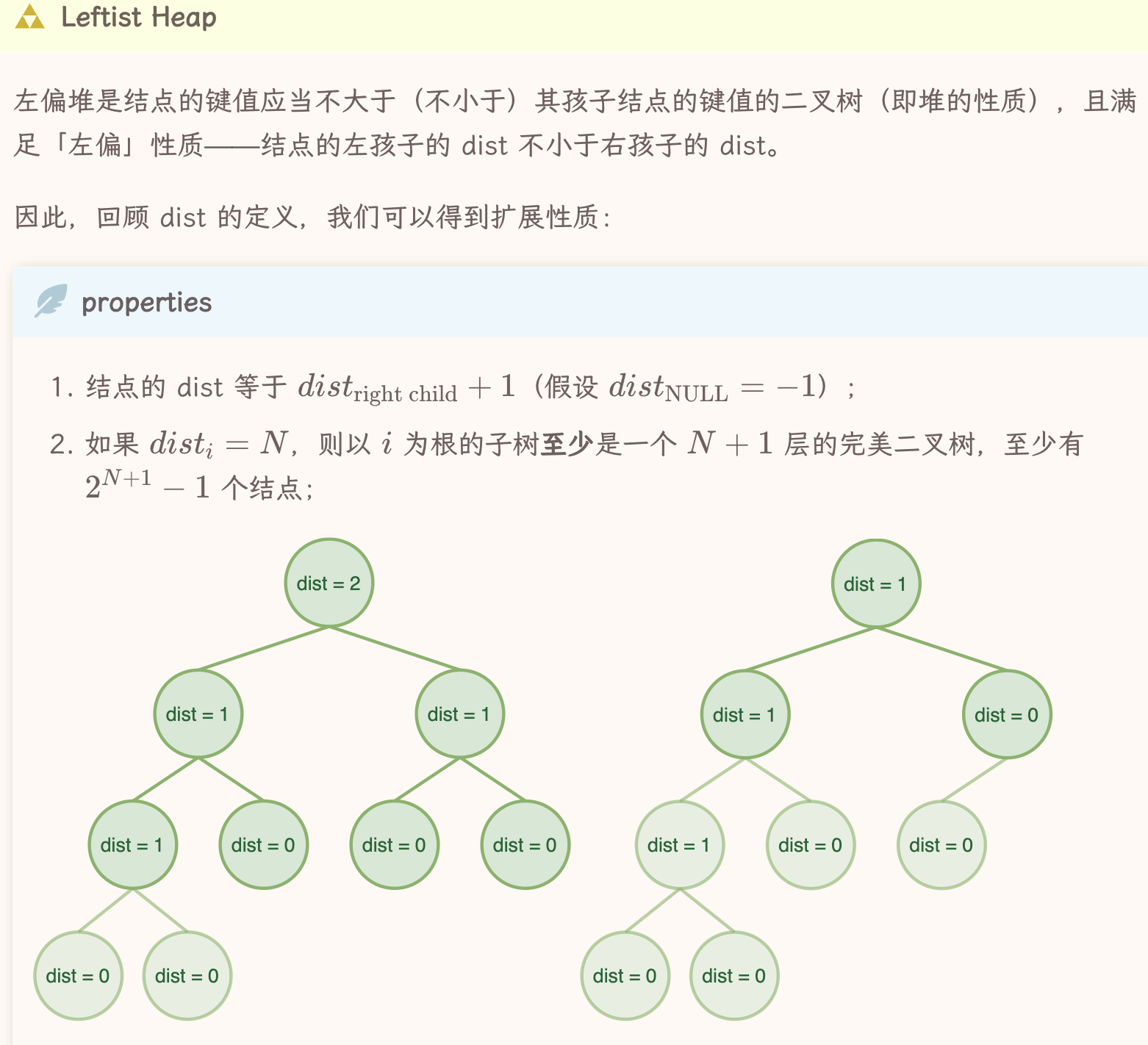

斜堆#

再来看斜堆的定义特点。 斜堆只定义了val,*rchild,*lchild,相比左偏堆少了对dist的维护。 斜堆的好处是能够快速合并，实现完全自上而下的并发操作。 下面讲merge操作：

操作：合并#

左偏堆#

先维护堆的性质，在回溯时维护左偏性质。 即先自上而下按照根的大小合并（根节点和左子树），再自下而上maintain（维护左偏性质，进行左右子树交换） 形式也分为两种方式：递归式和迭代式。迭代式需要额外维护两个指针，分别指向两棵树还没被合并 的子树的根，并不断选择较小的那个合并进去，直到两个指针都为空。

递归式代码：

LeftistHeapNode * merge(LeftistHeapNode * x, LeftistHeapNode * y) {
    if (x == NULL) return y;
    if (y == NULL) return x;
    if (x->val > y->val) {
        swap(x, y);
    }//小根堆
    x->rs = merge(x->rs, y);//自上而下合并
    if (x->ls->dist == NULL || x->ls->dist < x->rs->dist) {
        swap(x->ls, x->rs);
    }//维护交换根节点
    x->dist = x->rs->dist + 1;
    return x;
}

迭代式代码：

LeftistHeapNode * merge(LeftistHeapNode * x, LeftistHeapNode * y) {
    LeftistHeapNode * tx = x, * ty = y;
    LeftistHeapNode * res = NULL, * cur = NULL;
    while (tx != NULL && ty != NULL) {
        if (tx->val > ty->val) {
            swap(tx, ty);
        }
        if (res == NULL) {//res保留返回的根节点
            res = tx;
            cur = tx;
        } else {
            cur->rs = tx;
            cur = cur->rs;//合并
        }
        tx = tx->rs;//递归
    }
    while (ty != NULL) {
        if (res == NULL) {
            res = ty;
            cur = ty;
        } else {
            cur->rs = ty;
            cur = cur->rs;
        }
        ty = ty->rs;
    }
    res = adjust(res);
    return res;
}

迭代式有些很好的动画，方便理解：修佬的笔记

斜堆#

最大的区别：合并后无条件交换

摊还分析 ：斜堆#

• 势能函数：Φ(Heap)=number of heavy node in Heap
  • 对于一个子堆 H，如果右子堆大小+1 ≥ 整个堆大小$*(1/2)$（左边+1是因为包括根节点） ，则 H 是heavy node，否则是light node。 摊还证明： 至于为什么light nodes的数量是$O(logN)$，课堂上已经证明过（可以预设light nodes最多的情况来作图，数学归纳法证明。

习题#

F 考点：skew heap, merge 操作, amortized cost计算, potential functions记忆

补充：左偏堆单点删除#

（这个也忘记了，盘一下细节） 操作：只需要合并被删除的结点的两个子结点，得到新的树根节点去代替被删除的结点，再在回溯的过程中 bottom-up 地更新 dist 即可。 回溯maintain的过程：只要从新根节点开始检查/交换，因为左偏堆的子树都是左偏堆

代码实现：

LeftistHeapNode * del(LeftistHeapNode * cur, ElementType x) {
    if (cur->val == x) {
        return merge(cur->l, cur->r);
    } else {
        if (cur->val > x) return cur;//小根堆，找不到就返回cur指针
        if (cur->l != NULL) del(cur->l, x);
        if (cur->r != NULL) del(cur->r, x);
        adjust(cur);//回溯操作
    }
}

Divide && Conquer 时间复杂度计算（公式）#

直接看修佬笔记

总结一下： 三类方法：代换法、递归树法、主方法

主方法形式三#

考试一般会用到的是主方法第三种形式：

其他形式&方法的理解#

• 代换法：先猜后证，证明时用放缩方法。
• 递归树法：等比数列求和；画出图
  • 可能需要运用数学工具：（巧记：最上面和最下面换一下）
• 主方法形式一（有人能记住吗）
• 主方法形式二