1301 字
7 分钟
【ADS】作业1 AVL Tree Insertions
章节目标:代码(完成),操作(图)(完成),时间复杂度分析,均摊代价分析过程,和其他树的对比。
AVL树
.png)
.png)
.png)
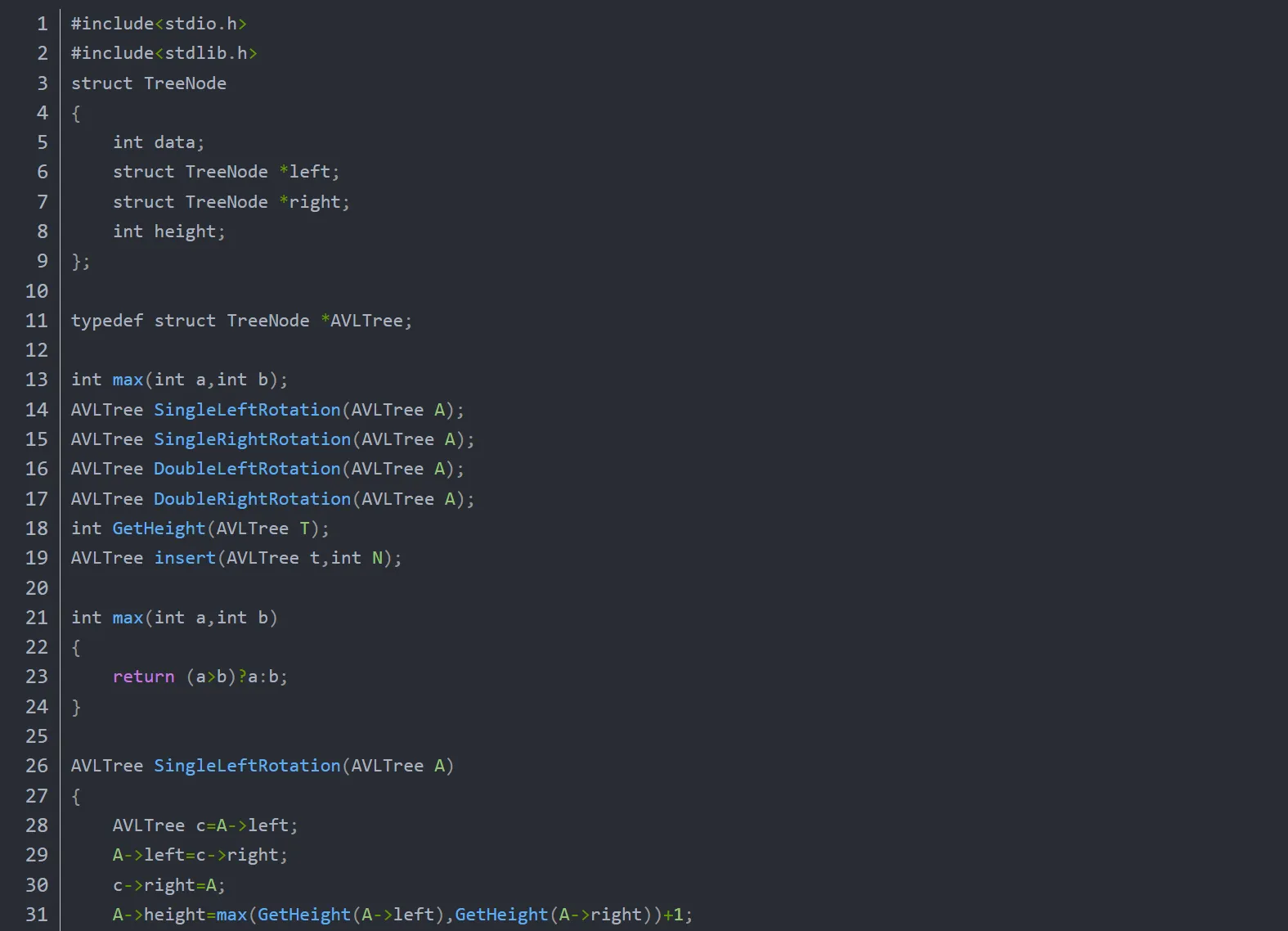
AVL树节点结构定义及基本操作:
#include <stdio.h>
#include <stdlib.h>
typedef struct Node {
int val;
int height; // 节点的高度
struct Node *left, *right;
} Node;
// 获取节点高度
int getHeight(Node *node) {
return node ? node->height : 0;
}
// 获取平衡因子
int getBalanceFactor(Node *node) {
return node ? getHeight(node->left) - getHeight(node->right) : 0;
}
// 更新节点的高度
void updateHeight(Node *node) {
if (node) {
node->height = 1 + (getHeight(node->left) > getHeight(node->right) ? getHeight(node->left) : getHeight(node->right));
}
}
// 右旋转
Node* rightRotate(Node *y) {
Node *x = y->left;
Node *T2 = x->right;
x->right = y;
y->left = T2;
updateHeight(y);
updateHeight(x);
return x;
}
// 左旋转
Node* leftRotate(Node *x) {
Node *y = x->right;
Node *T2 = y->left;
y->left = x;
x->right = T2;
updateHeight(x);
updateHeight(y);
return y;
}
// 插入节点
Node* insert(Node* node, int key) {
if (node == NULL) {
Node* newNode = (Node*)malloc(sizeof(Node));
newNode->val = key;
newNode->left = newNode->right = NULL;
newNode->height = 1; // 新节点高度为1
return newNode;
}
if (key < node->val) {
node->left = insert(node->left, key);
} else if (key > node->val) {
node->right = insert(node->right, key);
} else {
// Duplicate keys are not allowed in AVL tree
return node;
}
updateHeight(node);
int balance = getBalanceFactor(node);
// 进行旋转调整
if (balance > 1 && key < node->left->val) {
return rightRotate(node); // 左左情况
}
if (balance < -1 && key > node->right->val) {
return leftRotate(node); // 右右情况
}
if (balance > 1 && key > node->left->val) {
node->left = leftRotate(node->left); // 左右情况
return rightRotate(node);
}
if (balance < -1 && key < node->right->val) {
node->right = rightRotate(node->right); // 右左情况
return leftRotate(node);
}
return node;
}
// 获取树的最小值
Node* getMinValueNode(Node* node) {
Node* current = node;
while (current->left != NULL) {
current = current->left;
}
return current;
}
// 删除节点
Node* deleteNode(Node* root, int key) {
if (root == NULL) {
return root; // 如果树为空
}
// 进行标准的BST删除
if (key < root->val) {
root->left = deleteNode(root->left, key);
} else if (key > root->val) {
root->right = deleteNode(root->right, key);
} else {
// 找到要删除的节点
if ((root->left == NULL) || (root->right == NULL)) {
Node* temp = root->left ? root->left : root->right;
if (temp == NULL) {
temp = root;
root = NULL; // 删除节点为叶子节点
} else {
*root = *temp; // 只有一个子节点
}
free(temp);
} else {
// 找到右子树的最小值
Node* temp = getMinValueNode(root->right);
root->val = temp->val; // 用最小值替换当前节点
root->right = deleteNode(root->right, temp->val); // 删除最小值节点
}
}
if (root == NULL) {
return root; // 如果树变为空
}
updateHeight(root);
int balance = getBalanceFactor(root);
// 进行旋转调整
if (balance > 1 && getBalanceFactor(root->left) >= 0) {
return rightRotate(root); // 左左情况
}
if (balance > 1 && getBalanceFactor(root->left) < 0) {
root->left = leftRotate(root->left); // 左右情况
return rightRotate(root);
}
if (balance < -1 && getBalanceFactor(root->right) <= 0) {
return leftRotate(root); // 右右情况
}
if (balance < -1 && getBalanceFactor(root->right) > 0) {
root->right = rightRotate(root->right); // 右左情况
return leftRotate(root);
}
return root;
}
// 主函数
int main() {
Node* root = NULL;
// 插入节点
root = insert(root, 30);
...
return 0;
}
注:结构体数组版本的AVL操作代码,见我的朋友 @静安 的博客:https://ja101617.github.io/posts/note-ads/#avl-trees
对比自己写的代码,收获:
- 做题尽可能拆解、化简思路。如双旋操作可以简化为两次单旋函数的调用。
- 尽可能包装函数,使得每个函数体内部简洁易懂。如max函数使用。
- insert函数:处理根结点为空的情况
- 整体思路:拆解(主函数),封装,化简意识。
- 循环和迭代很多时候是等价的,思考哪种方式更有利于实现。
Q:写算法难点:难以考虑到所有情况的实现?
Splay Tree
Splay相对于AVL的好处(为什么用Splay):不需要维护节点高度,直接通过旋转操作实现。
splay树基本操作代码:
#include <stdio.h>
#include <stdlib.h>
// 定义节点结构
typedef struct SplayNode {
int key;
struct SplayNode *left, *right;
} SplayNode;
// 创建新节点
SplayNode* createNode(int key) {
SplayNode* node = (SplayNode*)malloc(sizeof(SplayNode));
node->key = key;
node->left = node->right = NULL;
return node;
}
// 右旋
SplayNode* rightRotate(SplayNode* y) {
SplayNode* x = y->left;
y->left = x->right;
x->right = y;
return x;
}
// 左旋
SplayNode* leftRotate(SplayNode* x) {
SplayNode* y = x->right;
x->right = y->left;
y->left = x;
return y;
}
// 伸展操作,将 key 所在节点或最近节点伸展到根位置
SplayNode* splay(SplayNode* root, int key) {
if (root == NULL || root->key == key)
return root;
if (key < root->key) {
if (root->left == NULL) return root;
if (key < root->left->key) {
root->left->left = splay(root->left->left, key);
root = rightRotate(root);
} else if (key > root->left->key) {
root->left->right = splay(root->left->right, key);
if (root->left->right != NULL)
root->left = leftRotate(root->left);
}
return (root->left == NULL) ? root : rightRotate(root);
} else {
if (root->right == NULL) return root;
if (key > root->right->key) {
root->right->right = splay(root->right->right, key);
root = leftRotate(root);
} else if (key < root->right->key) {
root->right->left = splay(root->right->left, key);
if (root->right->left != NULL)
root->right = rightRotate(root->right);
}
return (root->right == NULL) ? root : leftRotate(root);
}
}
// 查找节点,并将其伸展到根节点
SplayNode* find(SplayNode* root, int key) {
return splay(root, key);
}
// 查找最大节点,并将其伸展到根节点
SplayNode* findMax(SplayNode* root) {
if (root == NULL) return NULL;
while (root->right != NULL)
root = root->right;
return splay(root, root->key);
}
// 插入节点
SplayNode* insert(SplayNode* root, int key) {
if (root == NULL) return createNode(key);
root = splay(root, key);
if (root->key == key) return root;
SplayNode* newNode = createNode(key);
if (key < root->key) {
newNode->right = root;
newNode->left = root->left;
root->left = NULL;
} else {
newNode->left = root;
newNode->right = root->right;
root->right = NULL;
}
return newNode;
}
// 删除节点
SplayNode* deleteNode(SplayNode* root, int key) {
if (root == NULL) return NULL;
root = splay(root, key);
if (root->key != key) return root;
SplayNode* temp;
if (root->left == NULL) {
temp = root;
root = root->right;
} else {
temp = root;
root = splay(root->left, key);
root->right = temp->right;
}
free(temp);
return root;
}
// 主函数
int main() {
SplayNode* root = NULL;
root = insert(root, 10);
...
return 0;
}
【ADS】作业1 AVL Tree Insertions
https://tillyendless.github.io/posts/ads作业1-avl-tree-insertions/
